9061. Secular reception
Agent Johnny English is back in action!
This time, the fearless agent and his
assistant Bof have been tasked with maintaining order at a charity event. Upon
entering the hall and surveying the scene, English realized that to get a
complete picture of what was happening, he would need to take a stroll around
the room, chat with the guests, and observe the waiters. After completing his
reconnaissance, English, confident in his success, decided to meet up with Bof
and impress him with his incredible analytical skills. Unfortunately, poor Bof
completely loses his way at social events, so he just slowly follows the
instructions of the senior agent.
The hall is a square on the coordinate
plane with sides of length 106, parallel
to the coordinate axes. The entrance is located in the lower left corner of the
square, at point O(0,
0). Agent English plans to
select several guests positioned at points with integer coordinates and greet
each of them in turn. He will not greet the same guest consecutively, but he
might occasionally make a mistake and return to a guest he has already greeted.
The trained agent moves at a speed of p
and greets guests instantly. Meanwhile, Bof, moving at a speed of q, is heading directly to the final point of the route
planned by English.
To avoid raising suspicions, Agent English
wants to find a route where he and Bof will arrive at the meeting point
simultaneously. Unfortunately, the agent does not have time to think through
the details of his brilliant plan, so it is up to you to handle that.
Given the speeds q and p, find any route that
starts at point (0,
0) and consists of
points with non-negative coordinates not exceeding 106. Moreover, the time taken to traverse the
route at speed q must equal the time taken to traverse the
same route at speed p.
Input. Two positive
integers q and p (1 ≤ q ≤ p ≤ 105) – the speeds of Bof
and Agent English, respectively.
Output. In the
first line, print the number n (2 ≤ n ≤ 100) of points in the route. In the following n lines, print pairs of integers x and y (0 ≤
x, y ≤ 106) – the coordinates
of the points in the order of traversal. The first point must be (0, 0). Points may repeat, but there must not be two
identical points in a row.
|
Sample
input 1 |
Sample output 1 |
|
1 2 |
4 0 0 2 0 2 1 2 0 |
|
|
|
|
Sample
input 2 |
Sample output 2 |
|
1 3 |
4 0 0 2 0 2 2 2 0 |
SOLUTION
constructive
Algorithm analysis
Johnny English and Bof reach the final
point simultaneously in time t. Johnny English covers a
distance s1 = p * t, while Bof covers a distance s2 = q * t. The ratio of the distances traveled is
equal to the ratio of the speeds: s1 / s2 = p
/ q.
Let's construct such paths constructively.
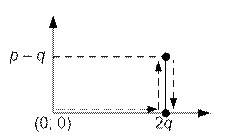
For example, consider a route consisting of 4 points: (0, 0) → (2q, 0) → (2q, p – q) → (2q, 0).
Here, the coordinate p – q is chosen to ensure that its value is non-negative
(according to the problem’s conditions, q ≤ p).
·
The
length of Johnny English’s path is 2q + 2 * (p – q) = 2p.
·
The
length of Bof’s path is 2q.
If the speeds of Johnny English and Bof are
the same, then the points (2q, 0) and (2q, p – q)
coincide, and according to the
problem’s conditions, there cannot be two identical points in a row on the
route. In this case, as a solution, one could choose, for example, the
following route: (0,
0) → (1, 0).
Algorithm realization
Read the
input data.
scanf("%d %d", &q, &p);
If the speeds of
Johnny English and Bof are the same, then they move from point (0, 0) to point (1, 1).
if (q == p)
{
printf("2\n");
printf("%d %d\n", 0, 0);
printf("%d %d\n", 1, 0);
return 0;
}
If p ≠ q, then the route consists of four points.
printf("4\n");
printf("%d %d\n", 0, 0);
printf("%d %d\n", 2 * q, 0);
printf("%d %d\n", 2 * q, p - q);
printf("%d %d\n", 2 * q, 0);